ずっと特性インピーダンスってものが謎だった。
50Ωとか75Ωとか言ってるけど、「インピーダンスなら周波数が関係すんじゃね?」とか、「ケーブルの長さだって関係あんじゃないの?」とかね。
わかってないけど、わかったフリしてこれまでどうにかやってこれた。
そういうことって多いと思う。
でも、ついにわかった(気になった)ので記事にしました。
要約
特性インピーダンスはインピーダンスなんだから、交流信号の周波数に影響されそうなものなのにどうもそうでもないようだ。また、ケーブルの長さとも関係が無いみたい。
はて面妖な?
どうやらそれは結局、特性インピーダンスの式
$$Z0= \frac{V}{I} = \sqrt{\frac{L}{C}}$$
の中に、周波数も長さのパラメータも無いことから推察できるのだけれど、
そもそもこの式ってどこから湧いてきたのよ?
ってことについて記している記事です。
おなじ疑問を抱いている方になら、ちょっとばかりお役に立てるかもしれません。
わたしと特性インピーダンスとの気まずい関係
仕事で映像信号を扱うことが多かったので、特性インピーダンスが50Ωの同軸ケーブルを使っていました。あんまり深く考えずにね。
プリント基板の引き込みのパターンも、同軸ケーブルに合わせて基板屋さんに50Ωで作ってもらっていた。
そのくせ特性インピーダンスが何なのか、よくわかっていないのだから恥ずかしい限りだ。
でもさぁ、こんな感じでも世の中ってケッコー渡って行けたりするんだよね。
だいたい、物理学だって3回くらい「何故?」を繰り返せば、現代の科学でわかっていない領域に入ることがほとんどだしね。(レベルが違うかな?)
セオリーどうりの部品を使っていればモノはできるので、
特性インピーダンスとは「そういうものだ」と思って思考停止した状態で仕事していても、ぶっコロされることも無く普通に生きてこれた。
だから、まぁそれでもいいちゃ良いのだ。
っていうかオレ、”のら犬頭”だからさ、目先の技術的なやっかいごとで一杯一杯でさ、優先度の低い特性インピーダンスのなんちゃらの解明は先送りにしていた。
でもこのたび雑記ブログを始めたことだし、速攻でネタ欠乏症にも陥ったしで、
これを良い機会だと捕らえてマジメに取り組んで記事にしてみようと思ったわけです。
特性インピーダンスの、なにが謎だと言うのか?

わたし的、特性インピーダンスの謎とは次の2項目
- インピーダンスなら周波数の影響を受けると思うんだけど?
50Ωとか75Ωって、特定の周波数での値なの?
たとえば100MHzのときのインピーダンスを基準にしているとか?
そうなんだろ? 違うんか? -
ケーブルって長さがイロイロなんだけど、長さの影響って受けないの?
10cmでも100cmでも同じなんか? なんで? んなわけなかろう?
とまぁこのように、青春の香りのする疑問がぼんやりと浮かんでは消えていた。
偉い人にありがちな、特性インピーダンスの説明
偉い人のHPに行って、特性インピーダンスについての解説を読むと、
たいてい次のように書かれている。
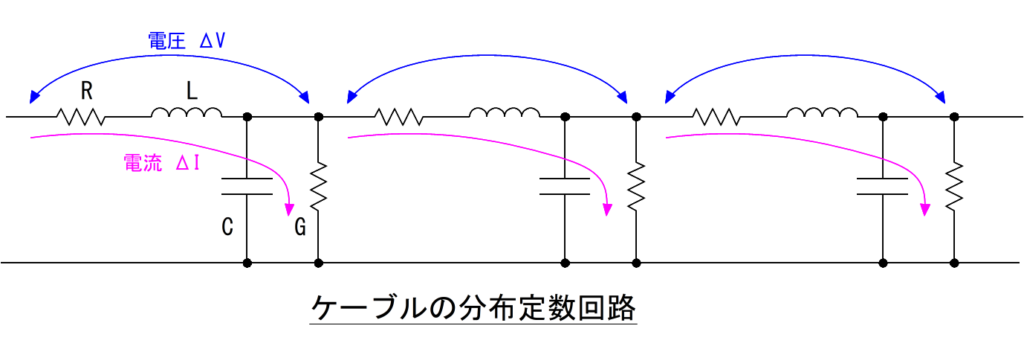
伝送線路の特性インピーダンスは、下に示す分布定数回路で表現できます。
そして、特性インピーダンスとは、
伝送線路上における信号の電圧と電流の比になります。
$$Z0= \frac{V}{I} = \sqrt{\frac{R+j\omega L}{G+j\omega C}}$$
直列に抵抗成分としてR、Cと並列にコンダクタンスGが含まれますが、
普通はこのRとGは無視できるほどの量なのでサクッと無視します。
すると以下に示すようにシンプルな式となるわけです。えっへん
$$Z0= \frac{V}{I} = \sqrt{\frac{L}{C}}$$
あーそうですか、はぁーー
でも、あれ? オイ、ちょっと待て
そもそもこの式ってどうやって出てきたんだ?
$$Z0= \frac{V}{I} = \sqrt{\frac{R+j\omega L}{G+j\omega C}}$$
偉い人はこれだから困るんだよ…
「普通わかるでしょ。当然」みたいなノリで、平気でミッシングリンクをぶち込んでくる…
のら犬は、これがわからなくて悩んでいました。
いつもは「おれにゃぁわかんね」と言ってアニメとか youtube とかに逃避するのですが、
今回は違います。ブログにしなきゃぁなりませんからね。
おじさんがんばっちゃいました。
無限伝送線路の特性インピーダンスを表す等式

考えたけどわからんかった… (;^ω^)
自分で考えるのは即座にあきらめてネットを漁りました

無限伝送線路の特性インピーダンス式の導き方
はい終了…
だと投げ槍すぎるし、万が一上記の賢人様のブログが閉鎖したりしたら困るので、かいつまんでパク×引用〇させていただくことにします。
次の枠内に記します。
※文章は完コピだとちょとムズムズするので、単純化した劣化コピーです。
※ぜひ素晴らしいオリジナルをご参照ください。
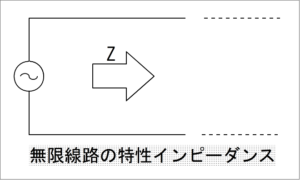
左の信号源から見て、伝送線路はインピーダンスZで無限に続いています。
この伝送線路には交流を流します。交流とは電圧電流が時間によって変化する信号ですね。
.
電線に変化する電流が流れると、変化する磁界が発生し、
それはつまりインダクタンス成分が存在することになります。
この単位長さ当たりのインダクタンスをL [H・m] とします。
.
同様に、2本の電線間には静電容量が発生するので、
この単位長さ当たりのキャパシタンスCを [F・m] とします。
.
ここで、微小な長さΔxに注目すると、以下の図ような等価回路が描けます。
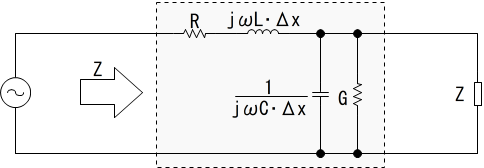
※R と G は、一般的には無視できる値なので無視します。式がゴチャつきますしね。
.
この図をインピーダンスZを表す等式にするとこのようになります。
$$Z= j\omega L \cdot\Delta x + \frac{1}{j\omega C\cdot\Delta x + \frac{1}{Z}}= j\omega L \cdot\Delta x + \frac{Z}{1+j\omega CZ \cdot\Delta x}$$
両辺に (1 + jωCZ・Δx) を掛けると
$$Z + j\omega C Z^2 \cdot\Delta x = j\omega L \cdot \Delta x – \omega^2 LCZ \cdot \Delta x^2 + Z$$
となるので、両辺からZを引いて Δxで割ると
$$j\omega CZ^2 = j\omega L – \omega^2 LCZ \cdot \Delta x$$
となります。
ここで
$$\Delta x \rightarrow 0$$
とすることで
$$j\omega CZ^2 = j\omega L$$
が得られ、特性インピーダンス Z は
$$z= \sqrt{\frac{L}{C}}$$
というシンプルな等式になります。
.
出典:『直列接続、並列接続の知識のみを使って特性インピーダンスを計算してみよう!』
$$Z0= \frac{V}{I} = \sqrt{\frac{L}{C}}$$
謎1: インピーダンスなら周波数の影響を受けると思うんだけど?
答え: 周波数の影響は受けない。(じつは、厳密には受ける)
特性インピーダンスの計算式の中に「ω」がありません。
ωが出てこないのだから、周波数の影響を受けようがないじゃないですか。
これの影響をうけるということ。
問題になりそうなときには、使うケーブルのデータシートを確認する必要がありますね。
謎2: ケーブルって長さがイロイロなんだけど、長さの影響って受けないの?
答え: ケーブルの長さの影響は受けない。(じつは、厳密には受ける)
ケーブルの長さが2倍になるとΔxが2倍になって、L も C も2倍になるものの、
$$Z0= \sqrt \frac{2L}{2C} = \sqrt \frac{L}{C}$$
という具合に分子と分母で相殺されてしまいます。
普通は無視できるから無問題。
まとめ

他力本願だったとはいえ、長年の謎が解明できました。
謎1: 周波数の影響は受けないのか? ← 受けない
謎2: ケーブルの長さの影響は受けないのか? ← 受けない
理由は、特性インピーダンスの式が以下のものだから。
$$Z0= \frac{V}{I} = \sqrt \frac{L}{C}$$
この式がすべてを物語っていたというわけでした。
「ネットの賢人さまありがとう」ってことです。
いい時代になったものだよ。
昔は何冊も本を買ってたもんな。それでもわかんなかった。(;^ω^)
最後まで読んでいただいて、ありがとうございました。m(_._)m